✨ 문제 상세


처음에는 각 도시를 거쳐서 갈 수 있는 다른 도시들의 수를 구한 후, 이를 기반으로 각 노드에 몇 대의 트럭이 필요한지를 결정함으로써 최종 비용을 계산하는 방법을 구상했다.
그러나 문제 의도에 비해 풀이 과정이 많이 복잡해지는 기분이 들어 새로운 방법을 시도하게 되었다.
🔍문제 풀이
문제의 예시를 참고해보자.
각 노드에 도착하는 트럭이 한 대씩 존재하므로, 여기서도 각 노드에 한 대씩 트럭을 보낸다고 가정하겠다.
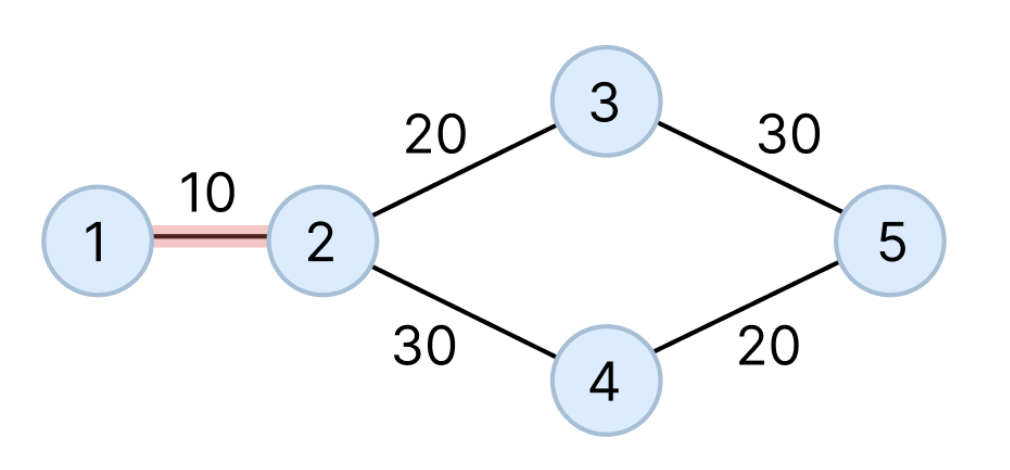
먼저, 2번노드까지의 최단 경로를 생각해보자.
자신이 첫번째이므로 따라갈 트럭이 없어 10이 된다.
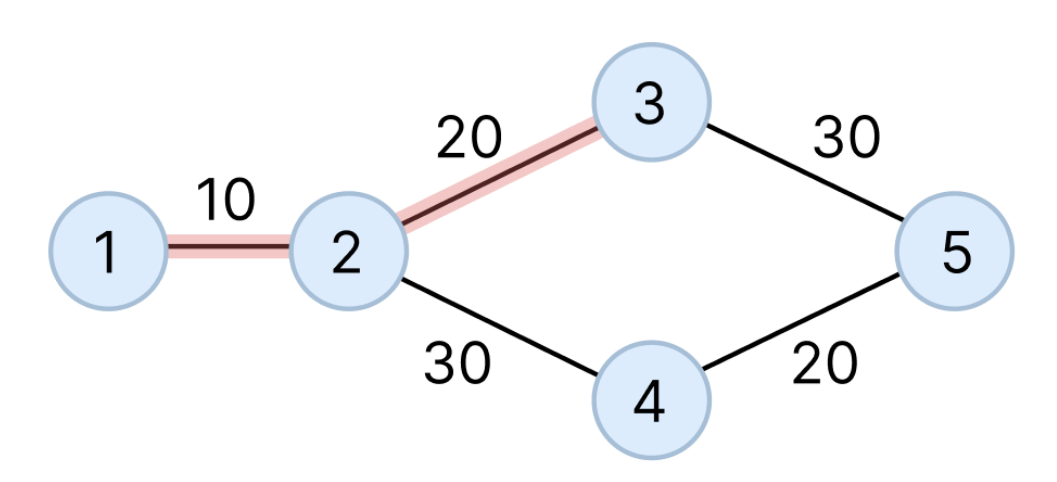
다음으로 3번 노드까지의 최단 경로를 보자.
2번까지는 위의 트럭과 함께 이동하면 되므로 90% 가격에 이동이 가능하다.
반면, 2번에서 3번으로 이동하는 도로는 처음으로 따라갈 트럭이 없으므로 100% 가격을 온전히 지불해야 한다.
- 1 → 2 : 10 * 0.9 = 9
- 2 → 3 : 20
- 총비용 : 9 + 20 = 29
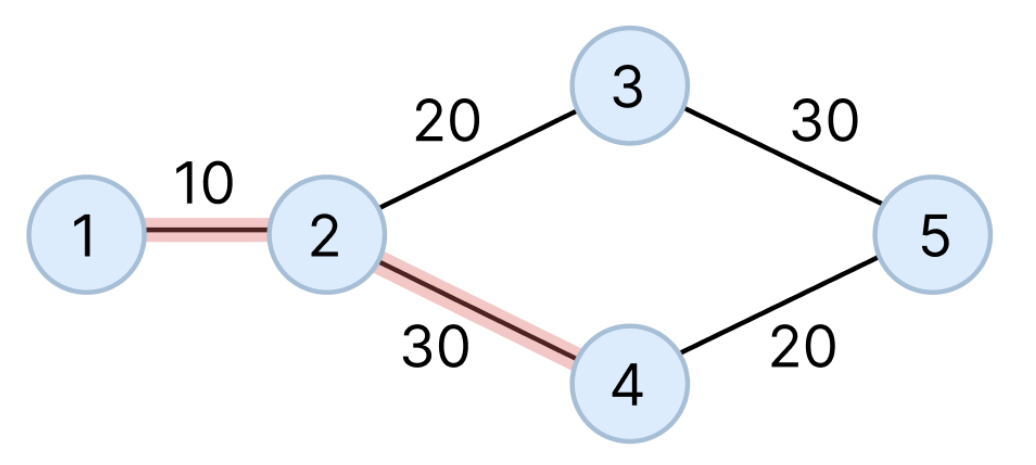
4번 노드까지의 최단 경로 또한 동일하다.
- 1 → 2 : 10 * 0.9 = 9
- 2 → 4 : 30
- 총비용 : 9 + 30 = 39
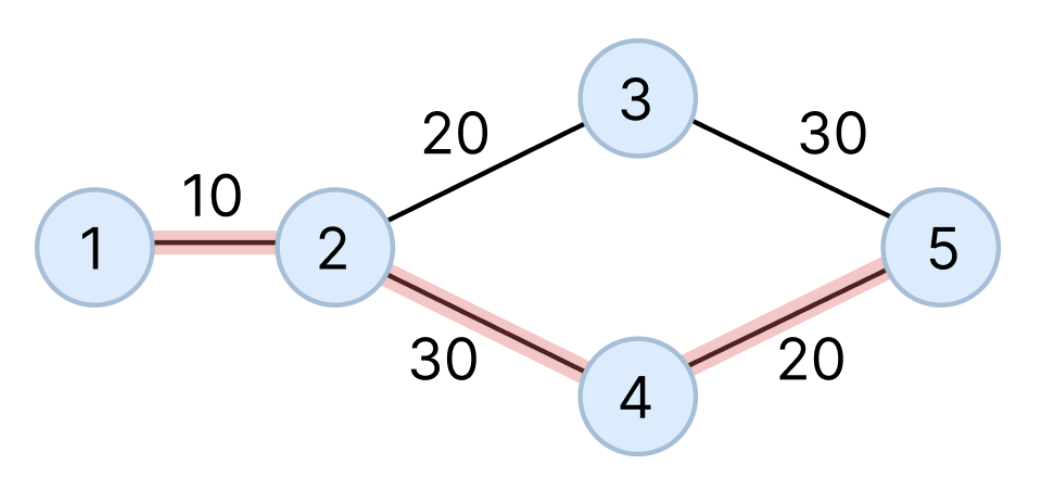
마지막으로 5번 노드까지의 최단 경로를 보자. 이 경우에는 총 2가지 경로를 사용할 수 있다.
- 1 → 2 → 3 → 5 : (10 * 0.9) + (20 * 0.9) + 30 = 57
(1에서 3까지의 경로 : 3번의 트럭을 따라가면 비용 절감 가능) - 1 → 2 → 4 → 5 : (10 * 0.9) + (30 * 0.9) + 20 = 56
(1에서 4까지의 경로 : 4번의 트럭을 따라가면 비용 절감 가능)
두 경로 모두 총 거리는 60으로 동일하므로, 최소 비용은 56이 된다.
위의 과정을 통해 아래의 결론을 얻을 수 있다.
- [ ... → N → M ] 의 경로를 통해 M번 노드로 가는 트럭은, 마지막 엣지를 제외하면 반드시 N번 노드로 가는 트럭과 동일한 경로를 사용 (최단이므로)
- N번 노드까지의 최소 비용을 구할 때, N번 노드로 진입하는 노드( = 마지막 엣지)를 제외하고는 90%로 계산 가능
- 즉, 총 비용은 1번 노드에서 각 노드까지의 최소 비용을 더한 값이 됨
다시 말해, 예시의 정답을 구하고 싶다면
- 1 → 2 : 10 = 10
- 1 → 3 : (10 * 0.9) + 20 = 29
- 1 → 4 : (10 * 0.9) + 30 = 39
- 1 → 5 : (10 * 0.9) + (30 * 0.9) + 20 = 56
⇒ 최종 cost = 10+29+39+56 = 134
와 같은 흐름으로 계산이 가능한 것이다.
❌ 코드 1 : 오답
정답 배열과 다익스트라에 사용되는 PQ에 서로 다른 값을 넣어줌으로써 계산 과정을 최소화하고자 했다.
- 정답 배열 : 직전 노드까지의 경로 90% + 마지막 경로 100% 저장
- PQ : (객체) 노드번호 / 해당 노드까지의 총 거리 90%
PQ에서 poll된 노드번호가 N이라 할 때, 저장된 cost는 N번을 지나 다른 노드로 가는 경우, 즉 이미 N번까지의 모든 도로가 사용된 후의 가격을 의미하므로 복잡한 과정 없이 빠른 계산이 가능할 것이라 생각했다.
🔽 틀린코드
public class BJ_31938 {
static final long INF = Long.MAX_VALUE;
static int N, M;
static long[] distance, answer;
static List<List<Node>> graph = new ArrayList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
for (int i = 0; i <= N; i++) {
graph.add(new ArrayList<>());
}
// 그래프 정보 입력받기
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph.get(s).add(new Node(e, c));
graph.get(e).add(new Node(s, c));
}
distance = new long[N+1];
answer = new long[N+1];
Arrays.fill(distance, INF);
dijkstra(1);
long total = 0L;
for (int i = 1; i <= N; i++) {
total += distance[i];
}
System.out.println(total);
}
public static void dijkstra (int start) {
PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparing(n -> n.cost));
boolean[] visited = new boolean[N+1];
pq.offer(new Node(start, 0));
distance[start] = 0;
while(!pq.isEmpty()) {
Node now = pq.poll();
// 선택 노드 방문 처리
if(visited[now.idx]) continue;
else visited[now.idx] = true;
for (Node next : graph.get(now.idx)) {
if(!visited[next.idx] && distance[next.idx] >= now.cost + next.cost) {
distance[next.idx] = now.cost + next.cost;
pq.add(new Node(next.idx, (long) (now.cost + (next.cost * 0.9))));
}
}
}
}
public static class Node {
int idx;
long cost;
public Node (int idx, long cost) {
this.idx = idx;
this.cost = cost;
}
}
}
당당하게 제출했지만 1%에서 바로 틀려버렸다....
🔍 틀린 이유
위의 코드에서 찾아볼 수 있는 반례는 다음과 같다.
3 3
1 2 1100
1 3 1100
2 3 20
// 정답 : 2200
// WA : 2110
문제를 잘 보면 트럭은 "최소 비용"이 아닌, "최단 거리"를 기준으로 이동한다고 적혀있다.
반례에서 1 → 3까지의 거리와 비용을 계산해보자.
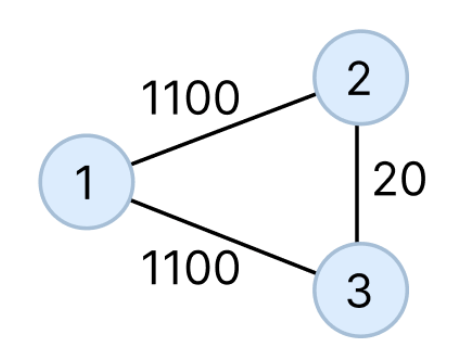
- 1 → 3
- 거리: 1100
- 비용: 1100 - 1 → 2 → 3
- 거리: 1120
- 비용: (1100 * 0.9) + 20 = 1010
문제의 조건대로라면, 트럭은 최단 거리로 이동하므로 1 → 2 → 3 경로를 사용할 수 없다.
그러나 위의 코드에서는 PQ에 전체 거리의 90%, 즉 990을 cost로 넣었기 때문에 기존 최단거리(1100) 보다 새로운 최단 거리(990+20)가 더 짧다고 판단해, 최종 비용을 갱신해버린다.
즉, 오차 없이 정확한 계산을 하기 위해서는 결국 총 거리와 총 비용 정보를 따로 저장해야 하는 것이었다...
✔️ 코드 2 : 정답
distance로는 실제 최단 거리를, answer로는 총 비용을 관리하도록 수정하였다.
이에 따라 PQ에서는 실제 거리를 기준으로 사용할 수 있게 되었다.
🔽 전체 코드
public class BJ_31938 {
static final long INF = Long.MAX_VALUE;
static int N, M;
static long[] distance, answer;
static List<List<Node>> graph = new ArrayList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
for (int i = 0; i <= N; i++) {
graph.add(new ArrayList<>());
}
// 그래프 정보 입력받기
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph.get(s).add(new Node(e, c));
graph.get(e).add(new Node(s, c));
}
distance = new long[N+1];
answer = new long[N+1];
Arrays.fill(distance, INF);
dijkstra(1);
long total = 0L;
for (int i = 1; i <= N; i++) {
total += answer[i];
}
System.out.println(total);
}
public static void dijkstra (int start) {
PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparing(n -> n.cost));
boolean[] visited = new boolean[N+1];
pq.offer(new Node(start, 0));
distance[start] = 0;
while(!pq.isEmpty()) {
Node now = pq.poll();
// 선택 노드 방문 처리
if(visited[now.idx]) continue;
else visited[now.idx] = true;
for (Node next : graph.get(now.idx)) {
long realCost = distance[now.idx] + next.cost;
// 미방문 && 새로운 distance가 최소인 경우(같아도 처리)
if(visited[next.idx] || distance[next.idx] < realCost) continue;
// 실제 거리(distance)는 같아도 감소한 거리값은 다를 수도 있음
// -> 같은 거리인 경우에도 업데이트 (savedCost는 항상 realCost보다 같거나 작으므로)
answer[next.idx] = (long) (distance[now.idx] * 0.9) + next.cost;
// 기존 경로(100%) 다익스트라 정보 갱신
distance[next.idx] = realCost;
pq.offer(new Node(next.idx, realCost));
}
}
}
public static class Node {
int idx;
long cost;
public Node (int idx, long cost) {
this.idx = idx;
this.cost = cost;
}
}
}
드디어 해결!